Boost.Bloom

Introduction

Boost.Bloom provides the class template boost::bloom::filter that can be configured to implement a classical Bloom filter as well as variations discussed in the literature such as block filters, multiblock filters, and more.

#include <boost/bloom.hpp>
#include <cassert>
#include <iostream>
#include <string>

int main()
{
  // Bloom filter of strings with 5 bits set per insertion
  using filter = boost::bloom::filter<std::string, 5>;

  // create filter with a capacity of 1'000'000 bits
  filter f(1'000'000);

  // insert elements (they can't be erased, Bloom filters are insert-only)
  f.insert("hello");
  f.insert("Boost");

  // elements inserted are always correctly checked as such
  assert(f.may_contain("hello") == true);

  // elements not inserted may incorrectly be identified as such with a
  // false positive rate (FPR) which is a function of the array capacity,
  // the number of bits set per element and generally how the boost::bloom::filter
  // was specified
  if(f.may_contain("bye")) { // likely false
    std::cout << "false positive\n";
  }
  else {
    std::cout << "everything worked as expected\n";
  }
}

The different filter variations supported are specified at compile time as part of the boost::bloom::filter instantiation definition. Boost.Bloom has been implemented with a focus on performance; SIMD technologies such as AVX2, Neon and SSE2 can be leveraged to speed up operations.

Getting Started

Consult the website section on how to install the entire Boost project or only Boost.Bloom and its dependencies.

Boost.Bloom is a header-only library, so no additional build phase is needed. C++11 or later required. The library has been verified to work with GCC 4.8, Clang 3.9 and Visual Studio 2015 (and later versions of those). You can check that your environment is correctly set up by compiling the example program shown above.

If you are not familiar with Bloom filters in general, see the primer; otherwise, you can jump directly to the tutorial.

Bloom Filter Primer

A Bloom filter (named after its inventor Burton Howard Bloom) is a probabilistic data structure where inserted elements can be looked up with 100% accuracy, whereas looking up for a non-inserted element may fail with some probability called the filter’s false positive rate or FPR. The tradeoff here is that Bloom filters occupy much less space than traditional non-probabilistic containers (typically, around 8-20 bits per element) for an acceptably low FPR. The greater the filter’s capacity (its size in bits), the lower the resulting FPR.

In general, Bloom filters are useful to prevent/mitigate queries against large data sets when exact retrieval is costly and/or can’t be made in main memory.

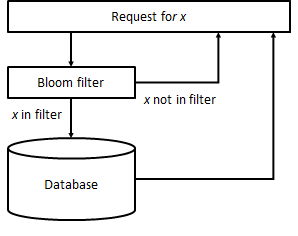
Example: Speeding up unsuccessful requests to a database

One prime application of Bloom filters and similar data structures is for the prevention of expensive disk/network accesses when these would fail to retrieve a given piece of information. For instance, suppose we are developing a frontend for a database with access time 10 ms and we know 50% of the requests will not succeed (the record does not exist). Inserting a Bloom filter with a lookup time of 200 ns and a FPR of 0.5% will reduce the average response time of the system from 10 ms to

(10 + 0.0002) × 50.25% + 0.0002 × 49.75% ≅ 5.03 ms,

that is, we get a ×1.99 overall speedup. If the database holds 1 billion records, an in-memory filter with say 8 bits per element will occupy 0.93 GB, which is perfectly realizable.

Figure 1. Improving DB negative access time with a Bloom filter.

Applications have been described in the areas of web caching, dictionary compression, network routing and genomics, among others. Broder and Mitzenmacher provide a rather extensive review of use cases with a focus on networking.

Implementation

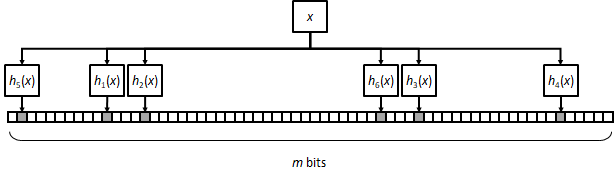
The implementation of a classical Bloom filter consists of an array of m bits, initially set to zero. Inserting an element x reduces to selecting k positions pseudorandomly (with the help of k independent hash functions) and setting them to one.

Figure 2. Insertion in a classical Bloom filter with k = 6 different hash functions. Inserting x reduces to setting to one the bits at positions 10, 14, 43, 58, 1, and 39 as indicated by h₁(x), … , h₆(x).

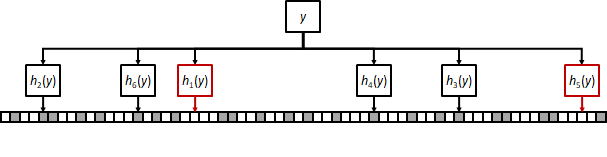
To check if an element y is in the filter, we follow the same procedure and see if the selected bits are all set to one. In the example figure there are two unset bits, which definitely indicates y was not inserted in the filter.

Figure 3. Lookup in a classical Bloom filter. Value y is not in the filter because bits at positions 20 and 61 are not set to one.

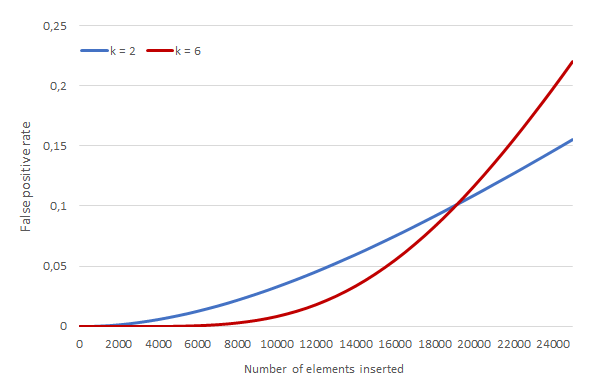
A false positive occurs when the bits checked happen to be all set to one due to other, unrelated insertions. The probability of having a false positive increases as we add more elements to the filter, whereas for a given number n of inserted elements, a filter with greater capacity (larger bit array) will have a lower FPR. The number k of bits set per operation also affects the FPR, albeit in a more complicated way: when the array is sparsely populated, a higher value of k improves (decreases) the FPR, as there are more chances that we hit a non-set bit; however, if k is very high the array will have more and more bits set to one as new elements are inserted, which eventually will reach a point where we lose out to a filter with a lower k and thus a smaller proportions of set bits. For given values of n and m, the optimum k is \(\lfloor k_{\text{opt}}\rfloor\) or \(\lceil k_{\text{opt}}\rceil\), with

\(k_{\text{opt}}=\displaystyle\frac{m\cdot\ln2}{n},\)

for a minimum FPR close to \(1/2^{k_{\text{opt}}} \approx 0.6185^{m/n}\). See the appendix on FPR estimation for more details.

Figure 4. FPR vs. number of inserted elements for two filters with m = 10⁵ bits. k = 6 (red) has a better (lower) FPR than k = 2 (blue) for small values of n, but eventually degrades more as n grows. The dotted line shows the minimum attainable FPR resulting from selecting the optimum value of k for each value of n.

Variations on the Classical Filter

Block Filters

An operation on a Bloom filter involves accessing k different positions in memory, which, for large arrays, results in k CPU cache misses and affects the operation’s performance. A variation on the classical approach called a block filter seeks to minimize cache misses by concentrating all bit setting/checking in a small block of b bits pseudorandomly selected from the entire array. If the block is small enough, it will fit in a CPU cacheline, thus drastically reducing the number of cache misses.

Figure 5. Block filter. A block of b bits is selected based on h₀(x), and all subsequent bit setting is constrained there.

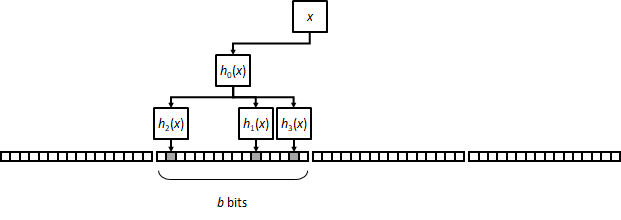
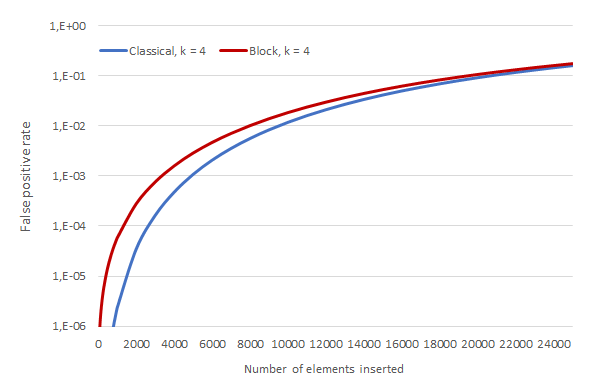
The downside is that the resulting FPR is worse than that of a classical filter for the same values of n, m and k. Intuitively, block filters reduce the uniformity of the distribution of bits in the array, which ultimately hurts their probabilistic performance.

Figure 6. FPR (logarithmic scale) vs. number of inserted elements for a classical and a block filter with the same k = 4, m = 10⁵ bits.

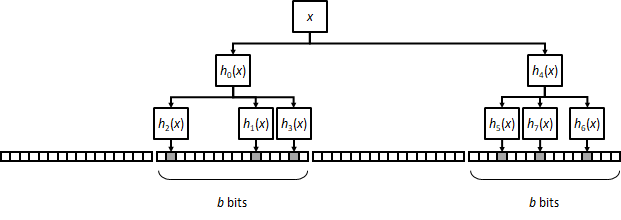
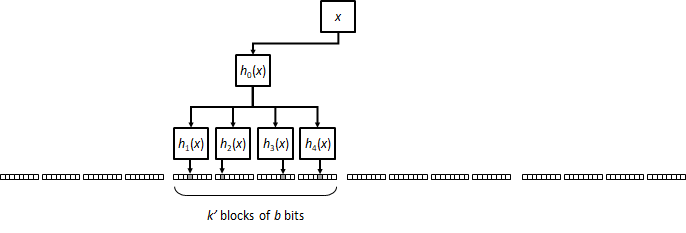
A further variation in this idea is to have operations select k blocks with k' bits set on each. This, again, will have a worse FPR than a classical filter with k·k' bits per operation, but improves on a plain k·k' block filter.

Figure 7. Block filter with multi-insertion. k = 2 blocks are selected, and k' = 3 bits are set in each.

Multiblock Filters

Multiblock filters take block filters' approach further by having bit setting/checking done on a sequence of consecutive blocks of size b, so that each block takes exactly one bit. This still maintains a good cache locality but improves FPR with respect to block filters because bits set to one are more spread out across the array.

Figure 8. Multiblock filter. A range of k' = 4 consecutive blocks is selected based on h₀(x), and a bit is set to one in each of the blocks.

Multiblock filters can also be combined with multi-insertion. In general, for the same number of bits per operation and equal values of n and m, a classical Bloom filter will have the better (lower) FPR, followed by multiblock filters and then block filters. Execution speed will roughly go in the reverse order. When considering block/multiblock filters with multi-insertion, the number of available configurations grows quickly and you will need to do some experimenting to locate your preferred point in the (FPR, capacity, speed) tradeoff space.

Tutorial

A boost::bloom::filter can be regarded as a bit array divided into subarrays that are selected pseudo-randomly (based on a hash function) upon insertion: each of the subarrays is passed to a subfilter that marks several of its bits according to some associated strategy.

Note that although boost::bloom::filter mimics the interface of a container and provides operations such as insert, it is actually not a container: for instance, insertion does not involve the actual storage of the element in the data stucture, but merely sets some bits in the internal array based on the hash value of the element.

Filter Definition

template<
  typename T, std::size_t K,
  typename Subfilter = block<unsigned char, 1>, std::size_t Stride = 0,
  typename Hash = boost::hash<T>,
  typename Allocator = std::allocator<unsigned char>
>
class filter;

T: Type of the elements inserted.
K: Number of subarrays marked per insertion.
Subfilter: Type of subfilter used.
Stride: Distance in bytes between the initial positions of consecutive subarrays.
Hash: A hash function for T.
Allocator: An allocator for unsigned char.

`Subfilter`

A subfilter defines the local strategy for setting or checking bits within a selected subarray of the bit array. It determines how many bits are modified per operation, how they are arranged in memory, and how memory is accessed. The following subfilters are provided:

Subfilter Description Pros Cons

Subfilter	Description	Pros	Cons
`block<Block, K'>`	Sets `K'` bits in a subarray of type `Block`	Very fast access time	FPR is worse (higher) the smaller `Block` is
`multiblock<Block, K'>`	Sets one bit in each of the elements of a `Block[K']` subarray	Better (lower) FPR than `block<Block, K'>` for the same `Block` type	Performance may worsen if cacheline boundaries are crossed when accessing the subarray
`fast_multiblock32<K'>`	Statistically equivalent to `multiblock<uint32_t, K'>`, but uses faster SIMD-based algorithms when SSE2, AVX2 or Neon are enabled at compile time	Always prefer it to `multiblock<uint32_t, K'>` when SSE2/AVX2/Neon is available	FPR is worse (higher) than `fast_multiblock64<K'>` for the same `K'`
`fast_multiblock64<K'>`	Statistically equivalent to `multiblock<uint64_t, K'>`, but uses a faster SIMD-based algorithm when AVX2 is enabled at compile time	Always prefer it to `multiblock<uint64_t, K'>` when AVX2 is available	Slower than `fast_multiblock32<K'>` for the same `K'`

block<Block, K'>

Sets K' bits in a subarray of type Block

Very fast access time

FPR is worse (higher) the smaller Block is

multiblock<Block, K'>

Sets one bit in each of the elements of a Block[K'] subarray

Better (lower) FPR than block<Block, K'> for the same Block type

Performance may worsen if cacheline boundaries are crossed when accessing the subarray

fast_multiblock32<K'>

Statistically equivalent to multiblock<uint32_t, K'>, but uses faster SIMD-based algorithms when SSE2, AVX2 or Neon are enabled at compile time

Always prefer it to multiblock<uint32_t, K'> when SSE2/AVX2/Neon is available

FPR is worse (higher) than fast_multiblock64<K'> for the same K'

fast_multiblock64<K'>

Statistically equivalent to multiblock<uint64_t, K'>, but uses a faster SIMD-based algorithm when AVX2 is enabled at compile time

Always prefer it to multiblock<uint64_t, K'> when AVX2 is available

Slower than fast_multiblock32<K'> for the same K'

In the table above, Block can be an unsigned integral type (e.g. unsigned char, uint32_t, uint64_t), or an array of 2^N unsigned integrals (e.g. uint64_t[8]). In general, the wider Block is, the better (lower) the resulting FPR, but cache locality worsens and performance may suffer as a result.

Note that the total number of of bits set/checked for a boost::bloom::filter<T, K, subfilter<…, K'>> is K * K'. The default configuration boost::bloom::filter<T, K> = boost::bloom::filter<T, K, block<unsigned char, 1>>, which corresponds to a classical Bloom filter, has the best (lowest) FPR among all filters with the same number of bits per operation, but is also the slowest: a new subarray is accessed for each bit set/checked. Consult the benchmarks section to see different tradeoffs between FPR and performance.

Once a subfilter have been selected, the parameter K' can be tuned to its optimum value (minimum FPR) if the number of elements that will be inserted is known in advance, as explained in a dedicated section; otherwise, low values of K' will generally be faster and preferred to higher values as long as the resulting FPR is at acceptable levels.

`Stride`

As we have seen, Subfilter defines the subarray (Block in the case of block<Block, K'>, Block[K'] for multiblock<Block, K'>) used by boost::bloom::filter: contiguous portions of the underlying bit array are then accessed and treated as those subarrays. The Stride parameter controls the distance in bytes between the initial positions of consecutive subarrays.

When the default value 0 is used, the stride is automatically set to the size of the subarrays, and so there’s no overlapping between them. If Stride is set to a smaller value than that size, contiguous subarrays superimpose on one another: the level of overlap is larger for smaller values of Stride, with maximum overlap happening when Stride is 1 byte.

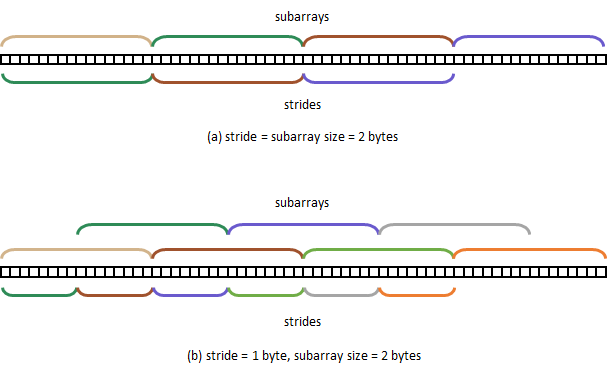
Figure 9. Two different configurations of Stride: (a) non-overlapping subarrays, (b) overlapping subarrays.
Each subarray is associated to the stride of the same color.

As it happens, overlapping improves (decreases) the resulting FPR with respect to the non-overlapping case, the tradeoff being that subarrays may not be aligned in memory, which can impact performance negatively.

`Hash`

Unlike other Bloom filter implementations requiring several hash functions per operation, boost::bloom::filter uses only one. By default, Boost.ContainerHash is used. Consult this library’s dedicated section if you need to extend boost::hash for your own types.

When the provided hash function is of sufficient quality, it is used as is; otherwise, a bit-mixing post-process is applied to hash values that improves their statistical properties so that the resulting FPR approaches its theoretical limit. The hash function is determined to be of high quality (more precisely, to have the so-called avalanching property) via the boost::hash_is_avalanching trait.

Capacity

The size of the filter’s internal array is specified at construction time:

using filter = boost::bloom::filter<std::string, 8>;
filter f(1'000'000); // array of 1'000'000 bits
std::cout << f.capacity(); // >= 1'000'000

Note that boost::bloom::filter default constructor specifies a capacity of zero, which in general won’t be of much use — the assigned array is null.

Instead of specifying the array’s capacity directly, we can let the library figure it out based on the number of elements we plan to insert and the desired FPR:

// we'll insert 100'000 elements and want a FPR ~ 1%
filter f(100'000, 0.01);

// this is equivalent
filter f2(filter::capacity_for(100'000, 0.01));

Be careful when the FPR specified is very small, as the resulting capacity may be too large to fit in memory:

// resulting capacity ~ 1.4E12, out of memory std::bad_alloc is thrown
filter f3(100'000, 1E-50);

Once a filter is constructed, its array is fixed (for instance, it won’t grow dynamically as elements are inserted). The only way to change it is by assignment/swapping from a different filter, or using reset:

f.reset(2'000'000); // change to 2'000'000 bits and clears the filter
f.reset(100'000, 0.005); // equivalent to reset(filter::capacity_for(100'000, 0.005));
f.reset(); // null array (capacity == 0)

Insertion and Lookup

Insertion is done in much the same way as with a traditional container:

f.insert("hello");
f.insert(data.begin(), data.end());

Of course, in this context "insertion" does not involve any actual storage of elements into the filter, but rather the setting of bits in the internal array based on the hash values of those elements. Lookup goes as follows:

bool b1 = f.may_contain("hello"); // b1 is true since we actually inserted "hello"
bool b2 = f.may_contain("bye"); // b2 is most likely false

As its name suggests, may_contain can return true even if the element has not been previously inserted, that is, it may yield false positives — this is the essence of probabilistic data structures. fpr_for provides an estimation of the false positive rate:

// we have inserted 100 elements so far, what's our FPR?
std::cout<< filter::fpr_for(100, f.capacity());

Note that in the example we provided the number 100 externally: boost::bloom::filter does not keep track of the number of elements that have been inserted — in other words, it does not have a size operation.

Once inserted, there is no way to remove a specific element from the filter. We can only clear up the filter entirely:

f.clear(); // sets all the bits in the array to zero

Filter Combination

boost::bloom::filters can be combined by doing the OR logical operation of the bits of their arrays:

filter f2 = ...;
...
f |= f2; // f and f2 must have exactly the same capacity

The result is equivalent to a filter "containing" the set union of the elements of f and f2. AND combination, on the other hand, results in a filter holding the intersection of the elements:

filter f3 = ...;
...
f &= f3; // f and f3 must have exactly the same capacity

For AND combination, be aware that the resulting FPR will be in general worse (higher) than if the filter had been constructed from scratch by inserting only the commom elements — don’t trust fpr_for in this case.

Direct Access to the Array

The contents of the bit array can be accessed directly with the array member function, which can be leveraged for filter serialization:

filter f1 = ...;
...

// save filter
std::ofstream out("filter.bin", std::ios::binary);
std::size_t c1=f1.capacity();
out.write(reinterpret_cast<const char*>(&c1), sizeof(c1)); // save capacity (bits)
boost::span<const unsigned char> s1 = f1.array();
out.write(reinterpret_cast<const char*>(s1.data()), s1.size()); // save array
out.close();

// load filter
filter f2;
std::ifstream in("filter.bin", std::ios::binary);
std::size_t c2;
in.read(reinterpret_cast<char*>(&c2), sizeof(c2));
f2.reset(c2); // restore capacity
boost::span<unsigned char> s2 = f2.array();
in.read(reinterpret_cast<char*>(s2.data()), s2.size()); // load array
in.close();

Note that array() is a span over unsigned chars whereas capacities are measured in bits, so array.size() is capacity() / CHAR_BIT. If you load a serialized filter in a computer other than the one where it was saved, take into account that the CPU architectures at each end must have the same endianness for the reconstruction to work.

Debugging

Visual Studio Natvis

Add the boost_bloom.natvis visualizer to your project to allow for user-friendly inspection of boost::bloom::filters.

Figure 10. View of a boost::bloom::filter with boost_bloom.natvis.

Choosing a Filter Configuration

Boost.Bloom offers a plethora of compile-time and run-time configuration options, so it may be difficult to make a choice. If you’re aiming for a given FPR or have a particular capacity in mind and you’d like to choose the most appropriate filter type, the following chart may come handy.

Figure 11. FPR vs. c for different filter types.

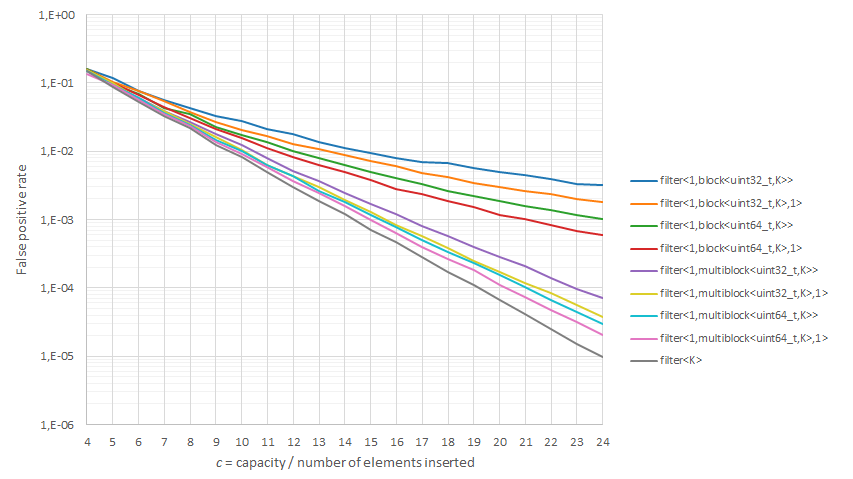
The chart plots FPR vs. c (capacity / number of elements inserted) for several boost::bloom::filters where K has been set to its optimum value (minimum FPR) as shown in the table below.

	c = capacity / number of elements inserted
	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24
`filter<T,1,block<uint32_t,K>>`	3	3	3	4	4	5	5	5	5	5	5	5	6	6	7	7	7	7	7	7	7
`filter<T,1,block<uint32_t,K>,1>`	2	3	4	4	4	4	5	5	5	6	6	6	6	6	6	6	7	7	7	7	7
`filter<T,1,block<uint64_t,K>>`	2	3	4	4	5	5	5	5	5	6	6	6	6	6	7	7	7	7	7	7	7
`filter<T,1,block<uint64_t,K>,1>`	2	3	4	4	4	5	6	6	6	7	7	7	7	7	8	8	8	8	8	9	9
`filter<T,1,multiblock<uint32_t,K>>`	3	3	4	5	6	6	8	8	8	8	9	9	9	10	13	13	15	15	15	16	16
`filter<T,1,block<uint64_t[8],K>>`	4	4	4	5	5	6	7	7	7	8	8	9	9	10	10	11	12	12	12	12	12
`filter<T,1,multiblock<uint32_t,K>,1>`	3	3	4	5	6	6	7	7	8	8	9	9	10	10	12	12	14	14	14	14	15
`filter<T,1,block<uint64_t[8],K>,1>`	3	3	4	5	6	6	7	7	7	8	8	8	10	11	11	12	12	12	12	12	13
`filter<T,1,multiblock<uint64_t,K>>`	4	4	5	5	6	6	6	7	8	8	10	10	12	13	14	15	15	15	15	16	17
`filter<T,1,multiblock<uint64_t,K>,1>`	3	3	4	5	5	6	6	7	9	10	10	11	11	12	12	13	13	13	15	16	16
`filter<T,K>`	3	4	4	5	5	6	6	8	8	9	10	11	12	13	13	13	14	16	16	16	17

Let’s see how this can be used by way of an example. Suppose we plan to insert 10M elements and want to keep the FPR at 10⁻⁴. The chart gives us five different values of c (the array capacity divided by the number of elements, in our case 10M):

filter<T, K> → c ≅ 19 bits per element
filter<T, 1, multiblock<uint64_t, K>, 1> → c ≅ 20 bits per element
filter<T, 1, multiblock<uint64_t, K>> → c ≅ 21 bits per element
filter<T, 1, block<uint64_t[8], K>, 1> → c ≅ 21 bits per element
filter<T, 1, multiblock<uint32_t, K>, 1> → c ≅ 21.5 bits per element
filter<T, 1, block<uint64_t[8], K>> → c ≅ 22 bits per element
filter<T, 1, multiblock<uint32_t, K>> → c ≅ 23 bits per element

These options have different tradeoffs in terms of space used and performance. If we choose filter<T, 1, multiblock<uint32_t, K>, 1> as a compromise (or better yet, filter<T, 1, fast_multiblock32<K>, 1>), the only remaining step is to consult the value of K in the table for c = 21 or 22, and we get our final configuration:

using my_filter=filter<std::string, 1, fast_multiblock32<14>, 1>;

The resulting filter can be constructed in any of the following ways:

// 1) calculate the capacity from the value of c we got from the chart
my_filter f((std::size_t)(10'000'000 * 21.5));

// 2) let the library calculate the capacity from n and target fpr
// expect some deviation from the capacity in 1)
my_filter f(10'000'000, 1E-4);

// 3) equivalent to 2)
my_filter f(my_filter::capacity_for(10'000'000, 1E-4));

Benchmarks

(More results in a dedicated repo.)

The tables show the false positive rate and execution times in nanoseconds per operation for several configurations of boost::bloom::filter<int, ...> where 10M elements have been inserted.

ins.: Insertion.
succ. lkp.: Successful lookup (the element is in the filter).
uns. lkp.: Unsuccessful lookup (the element is not in the filter, though lookup may return true).

Filters are constructed with a capacity c * N (bits), so c is the number of bits used per element. For each combination of c and a given filter configuration, we have selected the optimum value of K (that yielding the minimum FPR). Standard release-mode settings are used; AVX2 is indicated for Visual Studio builds (/arch:AVX2) and GCC/Clang builds (-march=native), which causes fast_multiblock32 and fast_multiblock64 to use their AVX2 variant.

GCC 14, x64

	`filter<int,K>`					`filter<int,1,block<uint64_t,K>>`					`filter<int,1,block<uint64_t,K>,1>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	6	2.1519	14.04	15.82	20.84	4	3.3467	5.82	6.50	6.54	5	3.0383	5.46	6.13	6.15
12	9	0.3180	47.65	52.28	27.38	5	1.0300	10.07	10.98	10.98	6	0.8268	11.52	12.52	12.49
16	11	0.0469	83.25	99.75	34.96	6	0.4034	18.34	18.38	18.39	7	0.2883	18.97	19.08	19.08
20	14	0.0065	125.12	135.16	39.56	7	0.1887	21.87	21.99	21.99	8	0.1194	22.85	25.21	25.17
	`filter<int,1,multiblock<uint64_t,K>>`					`filter<int,1,multiblock<uint64_t,K>,1>`					`filter<int,1,fast_multiblock32<K>>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	5	2.4510	6.42	7.10	7.12	5	2.3157	7.23	8.98	8.96	5	2.7361	5.90	5.67	5.70
12	8	0.4207	13.45	17.14	17.16	8	0.3724	16.49	20.61	20.65	8	0.5415	7.63	7.92	7.97
16	11	0.0764	29.25	30.26	30.26	11	0.0642	34.90	35.52	35.29	11	0.1179	19.11	20.64	14.95
20	13	0.0150	38.40	39.18	39.20	14	0.0122	40.68	50.85	50.24	13	0.0275	22.00	23.66	16.68
	`filter<int,1,fast_multiblock32<K>,1>`					`filter<int,1,fast_multiblock64<K>>`					`filter<int,1,fast_multiblock64<K>,1>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	5	2.4788	4.24	3.92	3.96	5	2.4546	5.59	5.86	5.89	5	2.3234	5.97	6.01	5.92
12	8	0.4394	8.19	8.03	8.03	8	0.4210	8.75	9.69	9.74	8	0.3754	11.13	12.23	12.20
16	11	0.0865	18.60	20.34	14.59	11	0.0781	24.65	25.86	21.31	11	0.0642	23.72	26.12	21.53
20	13	0.0178	21.80	23.56	16.42	13	0.0160	31.93	36.25	24.75	14	0.0110	31.64	36.52	25.04
	`filter<int,1,block<uint64_t[8],K>>`					`filter<int,1,block<uint64_t[8],K>,1>`					`filter<int,1,multiblock<uint64_t[8],K>>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	5	2.3292	7.58	8.62	15.62	6	2.2986	13.07	10.80	20.72	7	2.3389	15.28	15.27	15.29
12	7	0.4140	17.22	18.44	18.84	7	0.3845	22.19	21.28	20.79	10	0.3468	26.63	28.35	28.33
16	9	0.0852	27.39	27.86	21.79	10	0.0714	35.48	33.83	26.65	11	0.0493	45.00	49.14	49.05
20	12	0.0196	41.61	42.34	24.90	12	0.0152	50.90	50.31	28.79	15	0.0076	74.41	73.92	73.83

Clang 18, x64

	`filter<int,K>`					`filter<int,1,block<uint64_t,K>>`					`filter<int,1,block<uint64_t,K>,1>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	6	2.1519	13.57	14.12	20.85	4	3.3467	5.65	5.67	5.63	5	3.0383	5.42	6.03	5.98
12	9	0.3180	47.85	49.49	26.49	5	1.0300	11.03	10.97	10.98	6	0.8268	10.64	11.56	11.58
16	11	0.0469	83.54	85.35	31.09	6	0.4034	17.89	17.95	17.96	7	0.2883	17.23	19.07	19.08
20	14	0.0065	120.39	119.09	36.47	7	0.1887	21.98	21.72	21.72	8	0.1194	14.71	15.30	15.26
	`filter<int,1,multiblock<uint64_t,K>>`					`filter<int,1,multiblock<uint64_t,K>,1>`					`filter<int,1,fast_multiblock32<K>>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	5	2.4510	4.32	5.17	5.21	5	2.3157	4.10	4.63	4.66	5	2.7361	3.56	3.45	3.44
12	8	0.4207	8.83	10.55	10.56	8	0.3724	9.91	12.46	12.52	8	0.5415	7.85	7.54	7.54
16	11	0.0764	19.62	22.72	22.75	11	0.0642	19.05	22.93	22.92	11	0.1179	15.19	16.32	12.45
20	13	0.0150	23.87	29.73	29.79	14	0.0122	24.92	30.80	30.80	13	0.0275	17.36	18.34	13.99
	`filter<int,1,fast_multiblock32<K>,1>`					`filter<int,1,fast_multiblock64<K>>`					`filter<int,1,fast_multiblock64<K>,1>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	5	2.4788	3.72	3.38	3.36	5	2.4546	4.76	5.07	5.02	5	2.3234	5.27	5.37	5.25
12	8	0.4394	7.60	7.58	7.56	8	0.4210	8.66	9.24	9.27	8	0.3754	10.28	11.52	11.58
16	11	0.0865	14.43	16.09	11.92	11	0.0781	20.19	21.55	17.22	11	0.0642	18.83	21.05	16.85
20	13	0.0178	16.64	18.26	13.45	13	0.0160	25.12	29.48	20.08	14	0.0110	25.37	26.90	19.62
	`filter<int,1,block<uint64_t[8],K>>`					`filter<int,1,block<uint64_t[8],K>,1>`					`filter<int,1,multiblock<uint64_t[8],K>>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	5	2.3292	7.67	7.97	15.08	6	2.2986	13.91	10.27	19.76	7	2.3389	13.83	13.87	13.86
12	7	0.4140	17.06	15.61	17.52	7	0.3845	25.80	21.21	20.63	10	0.3468	31.17	32.58	32.61
16	9	0.0852	28.89	26.74	21.75	10	0.0714	36.21	32.66	24.97	11	0.0493	45.58	48.10	47.96
20	12	0.0196	43.30	35.81	24.25	12	0.0152	52.38	40.08	26.46	15	0.0076	78.06	72.34	72.55

Clang 15, ARM64

	`filter<int,K>`					`filter<int,1,block<uint64_t,K>>`					`filter<int,1,block<uint64_t,K>,1>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	6	2.1519	7.75	6.16	12.93	4	3.3467	2.05	1.99	2.00	5	3.0383	2.13	2.02	2.04
12	9	0.3180	13.15	11.04	16.16	5	1.0300	3.50	3.47	3.49	6	0.8268	3.22	3.16	3.09
16	11	0.0469	30.88	24.03	18.38	6	0.4034	6.66	6.31	6.56	7	0.2883	6.92	5.98	5.87
20	14	0.0065	53.83	40.29	20.91	7	0.1887	9.13	7.94	7.86	8	0.1194	7.69	6.46	6.74
	`filter<int,1,multiblock<uint64_t,K>>`					`filter<int,1,multiblock<uint64_t,K>,1>`					`filter<int,1,fast_multiblock32<K>>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	5	2.4510	2.70	2.48	2.56	5	2.3157	2.70	2.59	2.58	5	2.7361	2.38	2.49	2.50
12	8	0.4207	3.76	4.62	4.28	8	0.3724	4.31	4.64	4.53	8	0.5415	2.75	3.44	3.49
16	11	0.0764	10.95	9.92	9.78	11	0.0642	10.68	9.53	9.51	11	0.1179	8.69	8.41	5.77
20	13	0.0150	15.22	12.68	12.37	14	0.0122	14.96	12.90	12.72	13	0.0275	10.43	11.08	6.61
	`filter<int,1,fast_multiblock32<K>,1>`					`filter<int,1,fast_multiblock64<K>>`					`filter<int,1,fast_multiblock64<K>,1>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	5	2.4788	2.39	2.51	2.54	5	2.4510	2.72	2.51	2.55	5	2.3157	2.71	2.57	2.59
12	8	0.4394	2.94	3.10	3.03	8	0.4207	3.70	3.88	3.88	8	0.3724	4.26	4.68	4.39
16	11	0.0865	8.29	8.49	5.82	11	0.0764	10.94	9.88	9.73	11	0.0642	11.28	9.95	9.82
20	13	0.0178	10.41	10.88	6.60	13	0.0150	16.00	12.90	13.27	14	0.0122	15.77	13.47	13.55
	`filter<int,1,block<uint64_t[8],K>>`					`filter<int,1,block<uint64_t[8],K>,1>`					`filter<int,1,multiblock<uint64_t[8],K>>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	5	2.3292	4.64	4.30	11.29	6	2.2986	8.72	4.92	13.50	7	2.3389	8.87	6.65	6.71
12	7	0.4140	9.37	8.45	13.03	7	0.3845	13.33	7.80	12.91	10	0.3468	14.57	12.25	12.16
16	9	0.0852	16.42	13.68	14.25	10	0.0714	21.98	15.88	16.60	11	0.0493	26.05	21.96	23.13
20	12	0.0196	23.13	17.52	15.45	12	0.0152	28.91	22.21	17.26	15	0.0076	49.71	38.19	39.07

VS 2022, x64

	`filter<int,K>`					`filter<int,1,block<uint64_t,K>>`					`filter<int,1,block<uint64_t,K>,1>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	6	2.1519	11.10	11.87	15.76	4	3.3467	4.21	3.84	3.79	5	3.0383	4.72	4.58	4.52
12	9	0.3180	18.05	18.04	16.58	5	1.0300	6.22	5.70	5.67	6	0.8268	7.09	6.91	6.79
16	11	0.0469	68.24	79.45	25.94	6	0.4034	16.32	13.98	13.97	7	0.2883	16.42	16.00	16.02
20	14	0.0065	102.36	117.69	31.08	7	0.1887	20.87	19.33	19.26	8	0.1194	20.70	22.48	22.55
	`filter<int,1,multiblock<uint64_t,K>>`					`filter<int,1,multiblock<uint64_t,K>,1>`					`filter<int,1,fast_multiblock32<K>>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	5	2.4510	6.10	4.69	4.60	5	2.3157	8.57	5.05	4.97	5	2.7361	3.17	2.40	2.31
12	8	0.4207	10.18	8.79	8.59	8	0.3724	14.85	9.56	9.29	8	0.5415	4.81	4.92	4.34
16	11	0.0764	26.70	23.24	23.54	11	0.0642	29.69	27.85	27.90	11	0.1179	14.92	16.50	11.60
20	13	0.0150	36.05	34.93	35.15	14	0.0122	39.81	38.16	38.14	13	0.0275	16.37	17.89	12.37
	`filter<int,1,fast_multiblock32<K>,1>`					`filter<int,1,fast_multiblock64<K>>`					`filter<int,1,fast_multiblock64<K>,1>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	5	2.4788	3.18	2.26	2.16	5	2.4546	4.08	3.48	3.43	5	2.3234	4.17	3.40	3.33
12	8	0.4394	5.21	5.56	4.70	8	0.4210	6.73	6.13	5.67	8	0.3754	7.65	6.64	5.69
16	11	0.0865	15.06	15.45	10.99	11	0.0781	23.17	18.49	15.69	11	0.0642	20.82	19.11	16.18
20	13	0.0178	16.74	17.88	12.32	13	0.0160	28.66	26.92	18.97	14	0.0110	28.58	26.87	19.11
	`filter<int,1,block<uint64_t[8],K>>`					`filter<int,1,block<uint64_t[8],K>,1>`					`filter<int,1,multiblock<uint64_t[8],K>>`
c	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.	K	FPR [%]	ins.	succ. lkp.	uns. lkp.
8	5	2.3292	7.72	7.43	11.95	6	2.2986	10.68	9.72	14.95	7	2.3389	11.52	10.03	10.06
12	7	0.4140	11.37	12.06	13.71	7	0.3845	14.52	13.96	14.46	10	0.3468	15.45	14.39	14.26
16	9	0.0852	25.26	25.52	19.68	10	0.0714	33.28	32.53	20.02	11	0.0493	41.18	40.24	40.31
20	12	0.0196	35.58	34.62	22.93	12	0.0152	42.87	41.63	22.03	15	0.0076	68.99	64.79	64.87

Reference

`<boost/bloom.hpp>`

Convenience header including all the other headers listed in this reference.

`<boost/bloom/filter.hpp>`

Defines boost::bloom::filter and associated functions.

namespace boost{
namespace bloom{

template<
  typename T, std::size_t K,
  typename Subfilter = block<unsigned char, 1>, std::size_t Stride = 0,
  typename Hash = boost::hash<T>,
  typename Allocator = std::allocator<unsigned char>
>
class filter;

template<
  typename T, std::size_t K, typename SF, std::size_t S, typename H, typename A
>
bool operator==(
  const filter<T, K, SF, S, H, A>& x, const filter<T, K, SF, S, H, A>& y);

template<
  typename T, std::size_t K, typename SF, std::size_t S, typename H, typename A
>
bool operator!=(
  const filter<T, K, SF, S, H, A>& x, const filter<T, K, SF, S, H, A>& y);

template<
  typename T, std::size_t K, typename SF, std::size_t S, typename H, typename A
>
void swap(filter<T, K, SF, S, H, A>& x, filter<T, K, SF, S, H, A>& y)
  noexcept(noexcept(x.swap(y)));

} // namespace bloom
} // namespace boost

Class Template `filter`

boost::bloom::filter — A data structure that supports element insertion and probabilistic lookup, where an element can be determined to be in the filter with high confidence or else not be with absolute certainty. The probability that lookup erroneously classifies a non-present element as present is called the filter’s false positive rate (FPR).

boost::bloom::filter maintains an internal array of m bits where m is the filter’s capacity. Unlike traditional containers, inserting an element x does not store a copy of x within the filter, but rather results in a fixed number of bits in the array being set to one, where the positions of the bits are pseudorandomly produced from the hash value of x. Lookup for y simply checks whether all the bits associated to y are actually set.

For a given filter, the FPR increases as new elements are inserted.
For a given number of inserted elements, a filter with higher capacity has a lower FPR.

By convention, we say that a filter is empty if its capacity is zero or all the bits in the internal array are set to zero.

Synopsis

// #include <boost/bloom/filter.hpp>

namespace boost{
namespace bloom{

template<
  typename T, std::size_t K,
  typename Subfilter = block<unsigned char, 1>, std::size_t Stride = 0,
  typename Hash = boost::hash<T>,
  typename Allocator = std::allocator<unsigned char>
>
class filter
{
public:
  // types and constants
  using value_type                         = T;
  static constexpr std::size_t k           = K;
  using subfilter                          = Subfilter;
  static constexpr std::size_t stride      = see below;
  using hasher                             = Hash;
  using allocator_type                     = Allocator;
  using size_type                          = std::size_t;
  using difference_type                    = std::ptrdiff_t;
  using reference                          = value_type&;
  using const_reference                    = const value_type&;
  using pointer                            = value_type*;
  using const_pointer                      = const value_type*;

  // construct/copy/destroy
  filter();
  explicit filter(
    size_type m, const hasher& h = hasher(),
    const allocator_type& al = allocator_type());
  filter(
    size_type n, double fpr, const hasher& h = hasher(),
    const allocator_type& al = allocator_type());
  template<typename InputIterator>
    filter(
      InputIterator first, InputIterator last,
      size_type m, const hasher& h = hasher(),
      const allocator_type& al = allocator_type());
  template<typename InputIterator>
    filter(
      InputIterator first, InputIterator last,
      size_type n, double fpr, const hasher& h = hasher(),
      const allocator_type& al = allocator_type());
  filter(const filter& x);
  filter(filter&& x);
  template<typename InputIterator>
    filter(
      InputIterator first, InputIterator last,
      size_type m, const allocator_type& al);
  template<typename InputIterator>
    filter(
      InputIterator first, InputIterator last,
      size_type n, double fpr, const allocator_type& al);
  explicit filter(const allocator_type& al);
  filter(const filter& x, const allocator_type& al);
  filter(filter&& x, const allocator_type& al);
  filter(
    std::initializer_list<value_type> il,
    size_type m, const hasher& h = hasher(),
    const allocator_type& al = allocator_type());
  filter(
    std::initializer_list<value_type> il,
    size_type n, double fpr, const hasher& h = hasher(),
    const allocator_type& al = allocator_type());
  filter(size_type m, const allocator_type& al);
  filter(size_type n, double fpr, const allocator_type& al);
  filter(
    std::initializer_list<value_type> il,
    size_type m, const allocator_type& al);
  filter(
    std::initializer_list<value_type> il,
    size_type n, double fpr, const allocator_type& al);
  ~filter();
  filter& operator=(const filter& x);
  filter& operator=(filter&& x)
    noexcept(
	  std::allocator_traits<Allocator>::is_always_equal::value ||
      std::allocator_traits<Allocator>::propagate_on_container_move_assignment::value);
  filter& operator=(std::initializer_list<value_type> il);
  allocator_type get_allocator() const noexcept;

  // capacity
  size_type capacity() const noexcept;
  static size_type capacity_for(size_type n, double fpr);
  static double fpr_for(size_type n,size_type m)

  // data access
  boost::span<unsigned char>       array() noexcept;
  boost::span<const unsigned char> array() const noexcept;

  // modifiers
  void insert(const value_type& x);
  template<typename U>
    void insert(const U& x);
  template<typename InputIterator>
    void insert(InputIterator first, InputIterator last);
  void insert(std::initializer_list<value_type> il);

  void swap(filter& x)
    noexcept(std::allocator_traits<Allocator>::is_always_equal::value ||
             std::allocator_traits<Allocator>::propagate_on_container_swap::value);
  void clear() noexcept;
  void reset(size_type m = 0);
  void reset(size_type n, double fpr);

  filter& operator&=(const filter& x);
  filter& operator|=(const filter& x);

  // observers
  hasher hash_function() const;

  // lookup
  bool may_contain(const value_type& x) const;
  template<typename U>
    bool may_contain(const U& x) const;
};

} // namespace bloom
} // namespace boost

Description

Template Parameters

T

The cv-unqualified object type of the elements inserted into the filter.

K

Number of times the associated subfilter is invoked per element upon insertion or lookup. K must be greater than zero.

Subfilter

A subfilter type providing the exact algorithm for bit setting/checking into the filter’s internal array. The subfilter is invoked K times per operation on K pseudorandomly selected portions of the array (subarrays) of width used-value-size<Subfilter>.

Stride

Distance in bytes between the initial positions of consecutive subarrays. If Stride is specified as zero, the actual distance is automatically selected to used-value-size<Subfilter> (non-overlapping subarrays). Otherwise, Stride must be not greater than used-value-size<Subfilter>.

Hash

A Hash type over T.

Allocator

An Allocator whose value type is unsigned char.

Allocation and deallocation of the internal array is done through an internal copy of the provided allocator. If stride is a multiple of a = alignof(Subfilter::value_type), the array is byte-aligned to max(64, a).

If boost::hash_is_avalanching<Hash>::value is true and sizeof(std::size_t) >= 8, the hash function is used as-is; otherwise, a bit-mixing post-processing stage is added to increase the quality of hashing at the expense of extra computational cost.

Exception Safety Guarantees

Except when explicitly noted, all non-const member functions and associated functions taking boost::bloom::filter by non-const reference provide the basic exception guarantee, whereas all const member functions and associated functions taking boost::bloom::filter by const reference provide the strong exception guarantee.

Except when explicitly noted, no operation throws an exception unless that exception is thrown by the filter’s Hash or Allocator object (if any).

Types and Constants

static constexpr std::size_t stride;

Equal to Stride if that parameter was specified as distinct from zero. Otherwise, equal to used-value-size<subfilter>.

Constructors

Default Constructor

filter();

Constructs an empty filter using hasher() as the hash function and allocator_type() as the allocator.

Preconditions:	`hasher`, and `allocator_type` must be DefaultConstructible.
Postconditions:	`capacity() == 0`.

Capacity Constructor

explicit filter(
  size_type m, const hasher& h = hasher(),
  const allocator_type& al = allocator_type());
filter(
  size_type n, double fpr, const hasher& h = hasher(),
  const allocator_type& al = allocator_type());

Constructs an empty filter using copies of h and al as the hash function and allocator, respectively.

Preconditions:	`fpr` is between 0.0 and 1.0.
Postconditions:	`capacity() == 0` if `m == 0`, `capacity() >= m` otherwise (first overload). `capacity() == capacity_for(n, fpr)` (second overload).

Iterator Range Constructor

template<typename InputIterator>
  filter(
    InputIterator first, InputIterator last,
    size_type m, const hasher& h = hasher(),
    const allocator_type& al = allocator_type());
template<typename InputIterator>
  filter(
    InputIterator first, InputIterator last,
    size_type n, double fpr, const hasher& h = hasher(),
    const allocator_type& al = allocator_type());

Constructs a filter using copies of h and al as the hash function and allocator, respectively, and inserts the values from [first, last) into it.

Preconditions:	`InputIterator` is a LegacyInputIterator referring to `value_type`. `[first, last)` is a valid range. `fpr` is between 0.0 and 1.0.
Postconditions:	`capacity() == 0` if `m == 0`, `capacity() >= m` otherwise (first overload). `capacity() == capacity_for(n, fpr)` (second overload). `may_contain(x)` for all values `x` from `[first, last)`.

Copy Constructor

filter(const filter& x);

Constructs a filter using copies of x's internal array, x.hash_function() and std::allocator_traits<Allocator>::select_on_container_copy_construction(x.get_allocator()).

Postconditions:

*this == x.

Move Constructor

filter(filter&& x);

Constructs a filter tranferring x's internal array to *this and using a hash function and allocator move-constructed from x's hash function and allocator, respectively.

Postconditions:

x.capacity() == 0.

Iterator Range Constructor with Allocator

template<typename InputIterator>
  filter(
    InputIterator first, InputIterator last,
    size_type m, const allocator_type& al);
template<typename InputIterator>
  filter(
    InputIterator first, InputIterator last,
    size_type n, double fpr, const allocator_type& al);

Equivalent to filter(first, last, m, hasher(), al) (first overload) or filter(first, last, n, fpr, hasher(), al) (second overload).

Allocator Constructor

explicit filter(const allocator_type& al);

Constructs an empty filter using hasher() as the hash function and a copy of al as the allocator.

Preconditions:	`hasher` must be DefaultConstructible.
Postconditions:	`capacity() == 0`.

Copy Constructor with Allocator

filter(const filter& x, const allocator_type& al);

Constructs a filter using copies of x's internal array, x.hash_function() and al.

Postconditions:

*this == x.

Move Constructor with Allocator

filter(filter&& x, const allocator_type& al);

Constructs a filter tranferring x's internal array to *this if al == x.get_allocator(), or using a copy of the array otherwise. The hash function of the new filter is move-constructed from x's hash function and the allocator is a copy of al.

Postconditions:

x.capacity() == 0.

Initializer List Constructor

filter(
  std::initializer_list<value_type> il,
  size_type m, const hasher& h = hasher(),
  const allocator_type& al = allocator_type());
filter(
  std::initializer_list<value_type> il,
  size_type n, double fpr, const hasher& h = hasher(),
  const allocator_type& al = allocator_type());

Equivalent to filter(il.begin(), il.end(), m, h, al) (first overload) or filter(il.begin(), il.end(), n, fpr, h, al) (second overload).

Capacity Constructor with Allocator

filter(size_type m, const allocator_type& al);
filter(size_type n, double fpr, const allocator_type& al);

Equivalent to filter(m, hasher(), al) (first overload) or filter(n, fpr, hasher(), al) (second overload).

Initializer List Constructor with Allocator

filter(
  std::initializer_list<value_type> il,
  size_type m, const allocator_type& al);
filter(
  std::initializer_list<value_type> il,
  size_type n, double fpr, const allocator_type& al);

Equivalent to filter(il, m, hasher(), al) (first overload) or filter(il, n, fpr, hasher(), al) (second overload).

Destructor

~filter();

Deallocates the internal array and destructs the internal hash function and allocator.

Assignment

Copy Assignment

filter& operator=(const filter& x);

Let pocca be std::allocator_traits<Allocator>::propagate_on_container_copy_assignment::value. If pocca, replaces the internal allocator al with a copy of x.get_allocator(). If capacity() != x.capacity() or pocca && al != x.get_allocator(), replaces the internal array with a new one with capacity x.capacity(). Copies the values of x's internal array. Replaces the internal hash function with a copy of x.hash_function().

Preconditions:	If `pocca`, `Allocator` is nothrow CopyAssignable. `hasher` is nothrow Swappable.
Postconditions:	`*this == x`.
Returns:	`*this`.
Exception Safety:	Strong.

Move Assignment

filter& operator=(filter&& x)
  noexcept(
    std::allocator_traits<Allocator>::is_always_equal::value ||
    std::allocator_traits<Allocator>::propagate_on_container_move_assignment::value);

Let pocma be std::allocator_traits<Allocator>::propagate_on_container_move_assignment::value. If pocma, replaces the internal allocator with a copy of x.get_allocator(). If get_allocator() == x.get_allocator(), transfers x's internal array to *this; otherwise, replaces the internal array with a new one with capacity x.capacity() and copies the values of x's internal array. Replaces the internal hash function with a copy of x.hash_function().

Preconditions:	If `pocma`, `Allocator` is nothrow CopyAssignable. `hasher` is nothrow Swappable.
Postconditions:	`x.capacity() == 0`.
Returns:	`*this`.
Exception Safety:	Nothrow as indicated, otherwise strong.

Initializer List Assignment

filter& operator=(std::initializer_list<value_type> il);

Clears the filter and inserts the values from il.

Returns:

*this.

Capacity

size_type capacity() const noexcept;

Postconditions:	`capacity()` is a multiple of `CHAR_BIT`.
Returns:	The size in bits of the internal array.

Capacity Estimation

static size_type capacity_for(size_type n, double fpr);

Preconditions:	`fpr` is between 0.0 and 1.0.
Postconditions:	`filter(capacity_for(n, fpr)).capacity() == capacity_for(n, fpr)`. `capacity_for(n, 1.0) == 0`.
Returns:	An estimation of the capacity required by a `filter` to attain a false positive rate equal to `fpr` when `n` distinct elements have been inserted.

FPR Estimation

static double fpr_for(size_type n, size_type m);

Postconditions:	`fpr_for(n, m)` is between 0.0 and 1.0. `fpr_for(n, 0) == 1.0`. `fpr_for(0, m) == 0.0` (if `m != 0`).
Returns:	An estimation of the resulting false positive rate when `n` distinct elements have been inserted into a `filter` with capacity `m`.

Data Access

Array

boost::span<unsigned char>       array() noexcept;
boost::span<const unsigned char> array() const noexcept;

Postconditions:	`array().size() == capacity() / CHAR_BIT`.
Returns:	A span over the internal array.

Modifiers

Insert

void insert(const value_type& x);
template<typename U> void insert(const U& x);

If capacity() != 0, sets to one k * subfilter::k (not necessarily distinct) bits of the internal array deterministically selected from the value hash_function()(x).

Postconditions:	`may_contain(x)`.
Exception Safety:	Strong.
Notes:	The second overload only participates in overload resolution if `hasher::is_transparent` is a valid member typedef.

Insert Iterator Range

template<typename InputIterator>
  void insert(InputIterator first, InputIterator last);

Equivalent to while(first != last) insert(*first++).

Preconditions:

InputIterator is a LegacyInputIterator referring to value_type.
[first, last) is a valid range.

Insert Initializer List

void insert(std::initializer_list<value_type> il);

Equivalent to insert(il.begin(), il.end()).

Swap

void swap(filter& x)
  noexcept(std::allocator_traits<Allocator>::is_always_equal::value ||
           std::allocator_traits<Allocator>::propagate_on_container_swap::value);

Let pocs be std::allocator_traits<Allocator>::propagate_on_container_swap::value. Swaps the internal array and hash function with those of x. If pocs, swaps the internal allocator with that of x.

Preconditions:	`pocs \|\| get_allocator() == x.get_allocator()`. If `pocs`, `Allocator` is nothrow Swappable. `hasher` is nothrow Swappable.
Exception Safety:	Nothrow.

Clear

void clear() noexcept;

Sets to zero all the bits in the internal array.

Reset

void reset(size_type m = 0);
void reset(size_type n, double fpr);

First overload: Replaces the internal array if the resulting capacity calculated from m is not equal to capacity(), and clears the filter.
Second overload: Equivalent to reset(capacity_for(n, fpr)).

Preconditions:	`fpr` is between 0.0 and 1.0.
Postconditions:	In general, `capacity() >= m`. If `m == 0` or `m == capacity()` or `m == capacity_for(n, fpr)` for some `n` and `fpr`, then `capacity() == m`.
Exception Safety:	If `m == 0` or `capacity_for(n, fpr) == 0`, nothrow, otherwise strong.

Combine with AND

filter& operator&=(const filter& x);

If capacity() != x.capacity(), throws a std::invalid_argument exception; otherwise, changes the value of each bit in the internal array with the result of doing a logical AND operation of that bit and the corresponding one in x.

Preconditions:	The `Hash` objects of `x` and `y` are equivalent.
Returns:	`*this`;
Exception Safety:	Strong.

Combine with OR

filter& operator|=(const filter& x);

If capacity() != x.capacity(), throws an std::invalid_argument exception; otherwise, changes the value of each bit in the internal array with the result of doing a logical OR operation of that bit and the corresponding one in x.

Preconditions:	The `Hash` objects of `x` and `y` are equivalent.
Returns:	`*this`;
Exception Safety:	Strong.

Observers

get_allocator

allocator_type get_allocator() const noexcept;

Returns:

A copy of the internal allocator.

hash_function

hasher hash_function() const;

Returns:

A copy of the internal hash function.

Lookup

may_contain

bool may_contain(const value_type& x) const;
template<typename U> bool may_contain(const U& x) const;

Returns:	`true` iff all the bits selected by a hypothetical `insert(x)` operation are set to one.
Notes:	The second overload only participates in overload resolution if `hasher::is_transparent` is a valid member typedef.

Comparison

operator==

template<
  typename T, std::size_t K, typename S, std::size_t B, typename H, typename A
>
bool operator==(
  const filter<T, K, S, B, H, A>& x, const filter<T, K, S, B, H, A>& y);

Preconditions:	The `Hash` objects of `x` and `y` are equivalent.
Returns:	`true` iff `x.capacity() == y.capacity()` and `x`'s and `y`'s internal arrays are bitwise identical.

operator!=

template<
  typename T, std::size_t K, typename S, std::size_t B, typename H, typename A
>
bool operator!=(
  const filter<T, K, S, B, H, A>& x, const filter<T, K, S, B, H, A>& y);

Preconditions:	The `Hash` objects of `x` and `y` are equivalent.
Returns:	`!(x == y)`.

Swap

template<
  typename T, std::size_t K, typename S, std::size_t B, typename H, typename A
>
void swap(filter<T, K, S, B, H, A>& x, filter<T, K, S, B, H, A>& y)
  noexcept(noexcept(x.swap(y)));

Equivalent to x.swap(y).

Subfilters

A subfilter implements a specific algorithm for bit setting (insertion) and bit checking (lookup) for boost::bloom::filter. Subfilters operate on portions of the filter’s internal array called subarrays. The exact width of these subarrays is statically dependent on the subfilter type.

The full interface of a conforming subfilter is not exposed publicly, hence users can’t provide their own subfilters and may only use those natively provided by the library. What follows is the publicly available interface.

Subfilter::k

Result:

A compile-time std::size_t value indicating the number of (not necessarily distinct) bits set/checked per operation.

typename Subfilter::value_type

Result:

A cv-unqualified, TriviallyCopyable type to which the subfilter projects assigned subarrays.

Subfilter::used_value_size

Result:	A compile-time `std::size_t` value indicating the size of the effective portion of `Subfilter::value_type` used for bit setting/checking (assumed to begin at the lowest address in memory).
Postconditions:	Greater than zero and not greater than `sizeof(Subfilter::value_type)`.
Notes:	Optional.

used-value-size

template<typename Subfilter>
constexpr std::size_t used-value-size; // exposition only

used-value-size<Subfilter> is Subfilter::used_value_size if this nested constant exists, or sizeof(Subfilter::value_type) otherwise. The value is the effective size in bytes of the subarrays upon which a given subfilter operates.

`<boost/bloom/block.hpp>`

namespace boost{
namespace bloom{

template<typename Block, std::size_t K>
struct block;

} // namespace bloom
} // namespace boost

Class Template `block`

boost::bloom::block — A subfilter over an integral type.

Synopsis

// #include <boost/bloom/block.hpp>

namespace boost{
namespace bloom{

template<typename Block, std::size_t K>
struct block
{
  static constexpr std::size_t k = K;
  using value_type               = Block;

  // the rest of the interface is not public

} // namespace bloom
} // namespace boost

Description

Template Parameters

Block

An unsigned integral type or an array of 2^N elements of unsigned integral type.

K

Number of bits set/checked per operation. Must be greater than zero.

`<boost/bloom/multiblock.hpp>`

namespace boost{
namespace bloom{

template<typename Block, std::size_t K>
struct multiblock;

} // namespace bloom
} // namespace boost

Class Template `multiblock`

boost::bloom::multiblock — A subfilter over an array of an integral type.

Synopsis

// #include <boost/bloom/multiblock.hpp>

namespace boost{
namespace bloom{

template<typename Block, std::size_t K>
struct multiblock
{
  static constexpr std::size_t k = K;
  using value_type               = Block[k];

  // the rest of the interface is not public

} // namespace bloom
} // namespace boost

Description

Template Parameters

Block

An unsigned integral type or an array of 2^N elements of unsigned integral type.

K

Number of bits set/checked per operation. Must be greater than zero.

Each of the K bits set/checked is located in a different element of the Block[K] array.

`<boost/bloom/fast_multiblock32.hpp>`

namespace boost{
namespace bloom{

template<std::size_t K>
struct fast_multiblock32;

} // namespace bloom
} // namespace boost

Class Template `fast_multiblock32`

boost::bloom::fast_multiblock32 — A faster replacement of multiblock<std::uint32_t, K>.

Synopsis

// #include <boost/bloom/fast_multiblock32.hpp>

namespace boost{
namespace bloom{

template<std::size_t K>
struct fast_multiblock32
{
  static constexpr std::size_t k               = K;
  using value_type                             = implementation-defined;

  // might not be present
  static constexpr std::size_t used_value_size = implementation-defined;

  // the rest of the interface is not public

} // namespace bloom
} // namespace boost

Description

Template Parameters

`K`	Number of bits set/checked per operation. Must be greater than zero.

fast_multiblock32<K> is statistically equivalent to multiblock<std::uint32_t, K>, but takes advantage of selected SIMD technologies, when available at compile time, to perform faster. Currently supported: AVX2, little-endian Neon, SSE2. The non-SIMD case falls back to regular multiblock.

used-value-size<fast_multiblock32<K>> is 4 * K.

`<boost/bloom/fast_multiblock64.hpp>`

namespace boost{
namespace bloom{

template<std::size_t K>
struct fast_multiblock64;

} // namespace bloom
} // namespace boost

Class Template `fast_multiblock64`

boost::bloom::fast_multiblock64 — A faster replacement of multiblock<std::uint64_t, K>.

Synopsis

// #include <boost/bloom/fast_multiblock64.hpp>

namespace boost{
namespace bloom{

template<std::size_t K>
struct fast_multiblock64
{
  static constexpr std::size_t k               = K;
  using value_type                             = implementation-defined;

  // might not be present
  static constexpr std::size_t used_value_size = implementation-defined;

  // the rest of the interface is not public

} // namespace bloom
} // namespace boost

Description

Template Parameters

`K`	Number of bits set/checked per operation. Must be greater than zero.

fast_multiblock64<K> is statistically equivalent to multiblock<std::uint64_t, K>, but takes advantage of selected SIMD technologies, when available at compile time, to perform faster. Currently supported: AVX2. The non-SIMD case falls back to regular multiblock.

used-value-size<fast_multiblock64<K>> is 8 * K.

Future Work

A number of features asked by reviewers and users of Boost.Bloom are considered for inclusion into future versions of the library.

Bulk operations

Each insertion/lookup operation for boost::bloom::filter likely involves one or more cache misses in the access to the internal bit array. Following a similar approach to that of bulk visitation in Boost.Unordered, we can pipeline several operations so that cache miss stalls are leveraged to do useful computation. The interface for this functionality could be as follows:

f.insert(first1, last1);
f.may_contain(first2, last2, [] (const value_type& x, bool res) {
  // x is (likely) in the filter if res == true
});

`try_insert`

To avoid inserting an already present element, we now have to do:

if(!f.may_contain(x)) f.insert(x);

These two calls can be combined in a potentially faster, single operation:

bool res = f.try_insert(x); // returns true if x was not present

Estimation of number of elements inserted

For a classical Bloom filter, the number of elements actually inserted can be estimated from the number \(B\) of bits set to one in the array as

\(n\approx-\displaystyle\frac{m}{k}\ln\left(1-\displaystyle\frac{B}{m}\right),\)

which can be used for the implementation of a member function estimated_size. As of this writing, we don’t know how to extend the formula to the case of block and multiblock filters. Any help on this problem is much appreciated.

Run-time specification of k

Currently, the number k of bits set per operation is configured at compile time. A variation of (or extension to) boost::bloom::filter can be provided where the value of k is specified at run-time, the tradeoff being that its performance will be worse than the static case (preliminary experiments show an increase in execution time of around 10-20%).

Alternative filters

We can consider adding additional data structures such as cuckoo and xor filters, which are more space efficient and potentially faster.

Appendix A: FPR Estimation

For a classical Bloom filter, the theoretical false positive rate, under some simplifying assumptions, is given by

\(\text{FPR}(n,m,k)=\left(1 - \left(1 - \displaystyle\frac{1}{m}\right)^{kn}\right)^k \approx \left(1 - e^{-kn/m}\right)^k\) for large \(m\),

where \(n\) is the number of elements inserted in the filter, \(m\) its capacity in bits and \(k\) the number of bits set per insertion (see a derivation of this formula). For a fixed inverse load factor \(c=m/n\), the expression reaches at

\(k_{\text{opt}}=c\cdot\ln2\)

its minimum value \(1/2^{k_{\text{opt}}} \approx 0.6185^{c}\). The optimum \(k\), which must be an integer, is either \(\lfloor k_{\text{opt}}\rfloor\) or \(\lceil k_{\text{opt}}\rceil\).

In the case of filter of the form boost::bloom::filter<T, K, block<Block, K'>>, we can extend the approach from Putze et al. to derive the (approximate but very precise) formula:

\(\text{FPR}_{\text{block}}(n,m,b,k,k')=\left(\displaystyle\sum_{i=0}^{\infty} \text{Pois}(i,nbk/m) \cdot \text{FPR}(i,b,k')\right)^{k},\)

where

\(\text{Pois}(i,\lambda)=\displaystyle\frac{\lambda^i e^{-\lambda}}{i!}\)

is the probability mass function of a Poisson distribution with mean \(\lambda\), and \(b\) is the size of Block in bits. If we’re using multiblock<Block,K'>, we have

\(\text{FPR}_\text{multiblock}(n,m,b,k,k')=\left(\displaystyle\sum_{i=0}^{\infty} \text{Pois}(i,nbkk'/m) \cdot \text{FPR}(i,b,1)^{k'}\right)^{k}.\)

As we have commented before, in general

\(\text{FPR}_\text{block}(n,m,b,k,k') \geq \text{FPR}_\text{multiblock}(n,m,b,k,k') \geq \text{FPR}(n,m,kk'),\)

that is, block and multiblock filters have worse FPR than the classical filter for the same number of bits set per insertion, but they will be faster. We have the particular case

\(\text{FPR}_{\text{block}}(n,m,b,k,1)=\text{FPR}_{\text{multiblock}}(n,m,b,k,1)=\text{FPR}(n,m,k),\)

which follows simply from the observation that using {block|multiblock}<Block, 1> behaves exactly as a classical Bloom filter.

We don’t know of any closed, simple formula for the FPR of block and multiblock filters when Stride is not its "natural" size used-value-size<Subfilter>, that is, when subfilter subarrays overlap. We can use the following approximations (\(s\) = Stride in bits):

\(\text{FPR}_{\text{block}}(n,m,b,s,k,k')=\left(\displaystyle\sum_{i=0}^{\infty} \text{Pois}\left(i,\frac{n(2b-s)k}{m}\right) \cdot \text{FPR}(i,2b-s,k')\right)^{k},\)
\(\text{FPR}_\text{multiblock}(n,m,b,s,k,k')=\left(\displaystyle\sum_{i=0}^{\infty} \text{Pois}\left(i,\frac{n(2bk'-s)k}{m}\right) \cdot \text{FPR}\left(i,\frac{2bk'-s}{k'},1\right)^{k'}\right)^{k},\)

where the replacement of \(b\) with \(2b-s\) (or \(bk'\) with \(2bk'-s\) for multiblock filters) accounts for the fact that the window of hashing positions affecting a particular bit spreads due to overlapping. Note that the formulas reduce to the non-overlapping case when \(s\) takes its default value (\(b\) for block, \(bk'\) for multiblock). These approximations are acceptable for low values of \(k'\) but tend to underestimate the actual FPR as \(k'\) grows. In general, the use of overlapping improves (decreases) FPR by a factor ranging from 0.6 to 0.9 for typical filter configurations.

\(\text{FPR}_{\text{block}}(n,m,b,s,k,k')\) and \(\text{FPR}_\text{multiblock}(n,m,b,s,k,k')\) are the formulas used by the implementation of boost::filter::fpr_for.

Appendix B: Implementation Notes

Hash Mixing

This is the bit-mixing post-process we use to improve the statistical properties of the hash function when it doesn’t have the avalanching property:

\(m\leftarrow\text{mul}(h,C)\),
\(h'\leftarrow\text{high}(m)\text{ xor }\text{low}(m)\),

where \(\text{mul}\) denotes 128-bit multiplication of two 64-bit factors, \(\text{high}(m)\) and \(\text{low}(m)\) are the high and low 64-bit words of \(m\), respectively, \(C=\lfloor 2^{64}/\varphi \rfloor\) and \(\varphi\) is the golden ratio.

32-bit mode

Internally, we always use 64-bit hash values even if in 32-bit mode, where the user-provided hash function produces 32-bit outputs. To expand a 32-bit hash value to 64 bits, we use the same mixing procedure described above.

Dispensing with Multiple Hash Functions

Direct implementations of a Bloom filter with \(k\) bits per operation require \(k\) different and independent hash functions \(h_i(x)\), which incurs an important performance penalty, particularly if the objects are expensive to hash (e.g. strings). Kirsch and Mitzenmacher show how to relax this requirement down to two different hash functions \(h_1(x)\) and \(h_2(x)\) linearly combined as

\(g_i(x)=h_1(x)+ih_2(x).\)

Without formal justification, we have relaxed this even further to just one initial hash value \(h_0=h_0(x)\), where new values \(h_i\) are computed from \(h_{i-1}\) by means of very cheap mixing schemes. In what follows \(k\), \(k'\) are the homonym values in a filter of the form boost::bloom::filter<T, K, {block|multiblock}<Block, K'>>, \(b\) is sizeof(Block) * CHAR_BIT, and \(r\) is the number of subarrays in the filter.

Subarray Location

To produce a location (i.e. a number \(p\) in \([0,r)\)) from \(h_{i-1}\), instead of the straightforward but costly procedure \(p\leftarrow h_{i-1}\bmod r\) we resort to Lemire’s fastrange technique:

\(m\leftarrow\text{mul}(h_{i-1},r),\)
\(p\leftarrow\lfloor m/2^{64} \rfloor=\text{high}(m).\)

To decorrelate \(p\) from further uses of the hash value, we produce \(h_{i}\) from \(h_{i-1}\) as

\(h_i\leftarrow c \cdot h_{i-1} \bmod 2^{64}=\text{low}(c \cdot h_{i-1}),\)

with \(c=\text{0xf1357aea2e62a9c5}\) (64-bit mode), \(c=\text{0xe817fb2d}\) (32-bit mode) obtained from Steele and Vigna. The transformation \(h_{i-1} \rightarrow h_i\) is a simple multiplicative congruential generator over \(2^{64}\). For this MCG to produce long cycles \(h_0\) must be odd, so the implementation adjusts \(h_0\) to \(h_0'= (h_0\text{ or }1)\), which renders the least significant bit of \(h_i\) unsuitable for pseudorandomization (it is always one).

Bit selection

Inside a subfilter, we must produce \(k'\) values from \(h_i\) in the range \([0,b)\) (the positions of the \(k'\) bits). We do this by successively taking \(\log_2b\) bits from \(h_i\) without utilizing the portion containing its least significant bit (which is always one as we have discussed). If we run out of bits (which happens when \(k'> 63/\log_2b\)), we produce a new hash value \(h_{i+1}\) from \(h_{i}\) using the mixing procedure already described.

SIMD algorithms

`fast_multiblock32`

When using AVX2, we select up to 8 bits at a time by creating a __m256i of 32-bit values \((x_0,x_1,...,x_7)\) where each \(x_i\) is constructed from a different 5-bit portion of the hash value, and calculating from this the __m256i \((2^{x_0},2^{x_1},...,2^{x_7})\) with _mm256_sllv_epi32. If more bits are needed, we generate a new hash value as described before and repeat.

For little-endian Neon, the algorithm is similar but the computations are carried out with two uint32x4_ts in parallel as Neon does not have 256-bit registers.

In the case of SSE2, we don’t have the 128-bit equivalent of _mm256_sllv_epi32, so we use the following, mildly interesting technique: a __m128i of the form

\(((x_0+127)\cdot 2^{23},(x_1+127)\cdot 2^{23},(x_2+127)\cdot 2^{23},(x_3+127)\cdot 2^{23}),\)

where each \(x_i\) is in \([0,32)\), can be reinterpret_casted to (i.e., has the same binary representation as) the __m128 (register of floats)

\((2^{x_0},2^{x_1},2^{x_2},2^{x_3}),\)

from which our desired __m128i of shifted 1s can be obtained with _mm_cvttps_epi32.

`fast_multiblock64`

We only provide a SIMD implementation for AVX2 that relies in two parallel __m256is for the generation of up to 8 64-bit values with shifted 1s. For Neon and SSE2, emulation through 4 128-bit registers proved slower than non-SIMD multiblock<uint64_t, K>.

Release Notes

Boost 1.89

Initial release.

Acknowledgements

Peter Dimov and Christian Mazakas reviewed significant portions of the code and documentation during the development phase. Sam Darwin provided support for CI setup and documentation building.

The Boost acceptance review took place between the 13th and 22nd of May, 2025. Big thanks to Arnaud Becheler for his expert managing. The following people participated in the review: Dmitry Arkhipov, David Bien, Claudio DeSouza, Peter Dimov, Vinnie Falco, Alexander Grund, Seth Heeren, Andrzej Krzemieński, Ivan Matek, Christian Mazakas, Rubén Pérez, Kostas Savvidis, Peter Turcan, Tomer Vromen. Many thanks to all of them for their very helpful feedback.

Boost.Bloom was designed and written in Cáceres and Oropesa, January-June 2025.

Copyright and License

Of this documentation:

Distributed under the Boost Software License, Version 1.0.